

Proteins can be effective agents for catalysis and biochemical signaling, but to provide an appreciable shelf life, as needed in fields like regenerative medicine or biopharmaceuticals, one must stabilize these inherently labile species under dry, in-vitro conditions. Nevertheless, it is anticipated that proteinaceous- pharmaceuticals will account for half of all the new drugs in the next 10 to 20 years [ 1 ]. It is also understood that tissue scaffolds for regenerative medicine need to contain stabilized signaling protein or DNA. Protein preservation is becoming a critical technology. However, according to Robert Langer, Chair of the FDA’s Science Committee, improving protein stabilization technology is now one of the greatest challenges in the fields of biomaterials and pharmaceuticals.
Preservation can be achieved by embedding a protein in a glassy matrix, typically a polyalcohol or sugar. Ideally the stabilized protein is reconstituted under physiological conditions when its function is required. Unfortunately though, there is a loss of activity that increases as a function of storage time. Understanding the reasons for this loss of protein activity is a complex problem. From a thermodynamic perspective it is important that the preservation matrix have the ability to “replace” water in terms of the hydrogen bonding with the hydrophilic shell of the protein. However, water replacement alone is not sufficient; not all hydrogen bonding glass-forming compounds are effective preservation materials. In the present we illustrate the importance of dynamics in the glassy matrix for stabilizing proteins.
Previous studies showed that the stability of horseradish peroxidase ( HRP ) and yeast alcohol dehydrogenase ( Y A D H ) could be significantly improved embedding these proteins in glassy trehalose diluted with small amounts of glycerol [ 2 ]. Here we use the High Flux Backscattering Spectrometer ( HFBS ) and the Fermi-Chopper time-offlight Spectrometer ( FCS ) to illustrate that effective preservation is achieved through a suppression of picosecond to nanosecond relaxations and/or collective atomic vibrations. These local motions in the glass couple to the protein and suppress the necessary precursor motions that ultimately lead to larger scale motions that occur on the typical physiological time and length scales.
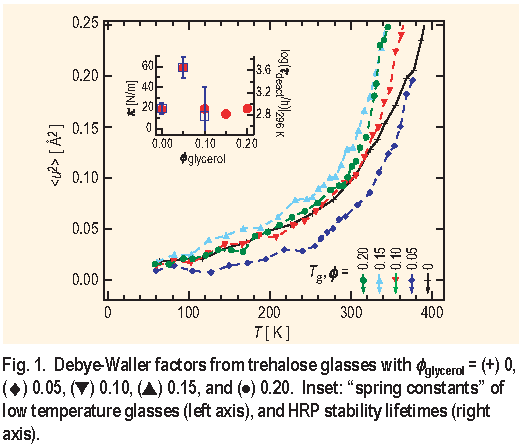
Figure 1 shows the hydrogen-weighted average mean square atomic displacement
for a series of lyophilized trehalose glasses diluted with increasing amounts of glycerol. The Q-dependence of the incoherent elastic scattering from the HFBS spectrometer is analyzed in terms of the Debye-Waller factor to extract
from a simple harmonic oscillator approximation, whereby
. As the temperature T increases there is a decrease in I elastic and
is simply proportional to the slope of ln ( I elastic ) vs Q2 at any given T. The 0.85 μe V energy resolution of the HFBS means that only motions faster than 200 MHz give rise to an increase of
; slower motions are seen as static.
The signatures of an effective preservation glass are immediately evident in the T dependence of
in Figure 1. Namely, the best protein preservation glass (
glycerol = 0.05 ) yields the smallest values of
. Below 250 K the nearly linear T dependence of
and the harmonic oscillator approximate can be used to calculate an effective spring constant (
) for the glass. The inset shows a pronounce peak in
( left axis ) at
glycerol = 0.05. The inset to Figure 1 also displays the time constant for degradation of HRP (
) in room-temperature trehalose glasses as a function of
glycerol. At
glycerol = 0.05, where the suppression of
is the greatest, the HRP stability is the greatest, more than five times better than the undiluted trehalose. While we do not show the data, the same effect is observed for Y A D H.
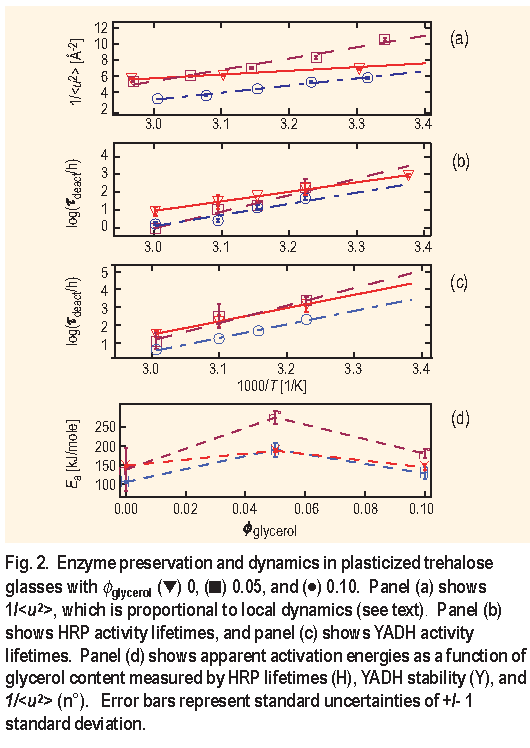
Parameters
(room T) and
( below 250 K ) are determined from different T regimes. To better correlate dynamics and preservation, Figure 2 parts ( a )-( c ) shows the 1/T dependencies of 1/
,
for H R P, and
for Y A D H over the same T regime. The motivation for Figure 2 ( a ) comes from the empirical observation that log ( viscosity ) is proportional to 1/
[ 3 ]. The data trends of panels ( a ) - ( c ) are summarized in panel ( d ) in terms of the apparent activation energies, E a, defined by the slopes of the lines. All three data sets show a maximum of E a at
glycerol = 0.05, indicating that suppressing the 200 GHz and faster dynamics of the glass leads to enhanced protein stability.
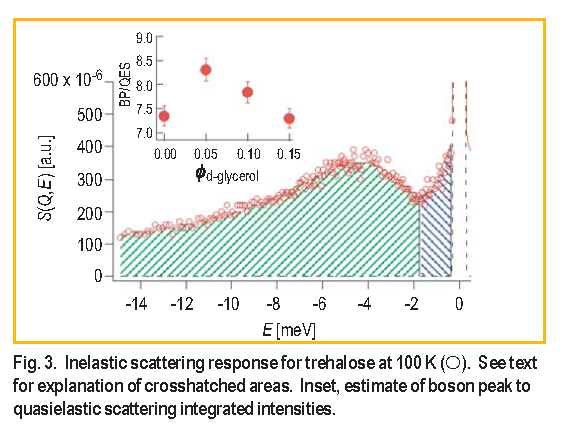
We can gain further insight into the dynamics that facilitate protein degradation by looking at the relative ratio of the relaxations reflected in the quasielastic scattering ( Q E S ) to the collective atomic vibrations boson peak intensities ( BP ). Figure 3 shows a typical S ( Q, E ) spectrum for trehalose at 100 K obtained from a FCS measurement.
The minimum in the spectrum at –1.7 m e V can be used, in a model-independent way, to delineate the relative strength of oscillatory and relaxational dynamics; integrating the green and blue areas provides a relative comparison of the BP and Q E S intensities respectively. In the inset to Figure 3 there is a maximum in the relative ratio of picosecond vibrations to relaxations at
glycerol = 0.05, coincident with the peaks in
and protein stability. The suppression of relaxations relative to the vibrations in the best preservation matrix is consistent with the fact that diffusive type motions ultimately lead to protein deactivation. These diffusive motions could be simple like the diffusion of a reactive gas through the matrix into the protein or complex like the irreversible unfolding of the protein.
We have shown for the first time that fast (
200 MHz ) dynamics of the host glass are crucial in stabilizing proteins. This is consistent with recent light scattering data that indicates that the protein dynamics couple to the glassy host, even in very viscous media [ 4 ]. When formulating a glassy matrix for preservation, it is important to tune the high frequency coupling such that the glass suppresses the protein dynamics. Previous folklore implied that high Tg glasses make better preservation materials. This was based on the notion that deeper in the glassy state the protein would be more effectively suspended in a vitreous state of animation. However, a higher Tg does not necessitate suppressed dynamics at the relevant pico- to nanosecond time scales, as illustrated here. Adding small amounts of glycerol to trehalose decreases the Tg, but yields a superior preservation matrix.
References:
[1] C. M. Henery, C&E News 78 (43), 85 (2000).
[2] M. T. Cicerone, A. Tellington, L. Trost, and A. Sokolov, BioProcess Intl. 1 (1), 23 (2003).
[3] U. Buchenau and R. Zorn, Europhys. Lett. 18 (6), 523 (1992).
[4] G. Caliskan, D. Mechtani, S. Azzam, A. Kisliuk, M. T. Cicerone and A. P. Sokolov, submitted.
M. T. Cicerone and C. L. Soles
Polymers Division
National Institute of Standards and Technology
Gaithersburg, MD 20899-8541
Back to FY2003 HTML main page
Go to previous article
Go to next article
To view all symbols correctly, please download Internet Explorer 6 or Netscape 7.1