A “Chinese” checkerboard having an equal number of black and white marbles cannot have every neighbor being the opposite kind, whereas a square checkerboard can. The triangular array on a Chinese checkerboard offers an example of “geometrical frustration”. Frustration (i.e., a condition in which some relation among the components cannot be satisfied simultaneously) is an important concept in understanding disordered states of matter. Systems in which a large diversity of states are involved are common in biology, chemistry and physics (Refer to references 1 and 2). Notable examples are glasses, liquids and proteins. Magnetic systems offer extreme examples of frustration in the form of spin lattices, where all interactions between spins cannot be simultaneously satisfied. Such geometrical frustration can lead to the emergence of qualitatively new states of matter, having “composite” degrees of freedom.
To explore this possibility, we examined magnetic fluctuations in zinc, chromium sub 2,
oxygen sub 4, (Refer to reference 3). The B-site of this spinel lattice occupied by spin
3 halves, chromium 3 plus, leads to a magnet with dominant nearest neighbor interactions on
the lattice of corner-sharing tetra hedra (Refer to reference 4) shown in Figure 1. Because
the spin interaction energy is minimized when the four spins on each tetra hedron add to zero,
interactions do not call for long-range order, but simply define a restricted phase space
for fluctuations. Just as composite fermions can emerge from degenerate Landau
levels in a two-dimensional electron gas, the near-degenerate manifold of states
in a frustrated magnet is fertile ground for emergent behavior (Refer to reference 5).
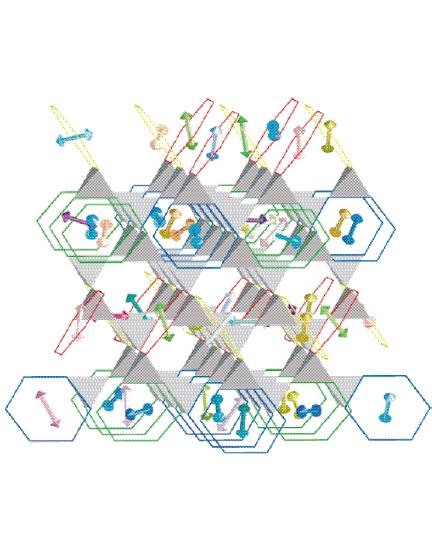
| Figure 1. The lattice of corner-sharing tetrahedra formed by the octahedrally coordinated B sites in a spinel structure with chemical formula A, B sub 2, O sub 4. A periodic assignment of all spins in the pyrochlore lattice is made to four different types of non-overlapping hexagons, represented by the colors blue, green, red, and gold. Every spin belongs to just one hexagon and each such hexagon carries a six-spin director. The resulting tetragonal structure of these hexagons has a unit cell of 2A, by 2A, by 3C, and can be described by a stacking of two different types of three-layer slabs along the c-axis. The hexagon coverage on consecutive slabs is in fact uncorrelated, so that a macroscopic number of random slab-sequences can be generated. |
Neutron scattering provides the most effective tool to study possible composite spin degrees of freedom by directly probing the form factor of such entities. Figure 2 (A, and B) show the wave vector dependence of the low energy inelastic neutron scattering cross section in the spin-liquid phase of zinc, chromiun sub 2, oxygen sub 4. The data exhibit broad maxima at the Brillouin zone boundaries, signaling the emergence of confined nano-scale spin clusters. Rather than Fourier-inverting the data, we consider potential spin clusters and test the corresponding prediction for the form factor against the data.
Individual tetra hedra would be prime candidates for such clusters, as they constitute the basic motif of the pyrochlore lattice. However, a tetra hedron is too small to account for the observed features. The next largest symmetric structural unit is the hexagonal loop formed by a cluster of six tetra hedra (Figure 3). Two spins of each tetra hedron occupy the vertices of a hexagon while the other two spins belong to different hexagons. It is possible to assign all spins on the spinel lattice to hexagons simultaneously, thus producing N over 6 weakly interacting degrees of freedom (Figure 1). An outstanding fit is achieved for the antiferromagnetic hexagonal spin loops, as displayed in Figure 2 (C and D). Thus, rather than scattering from individual spins, neutrons scatter from antiferromagnetic hexagonal spin clusters. In effect, zinc, chromiun sub 2, oxygen sub 4, at low temperatures is not a system of strongly interacting spins, but a protectorate of weakly interacting spin-loop directors. Since the six hexagon spins are anti-parallel with each other, the staggered magnetization vector for a single hexagon, which shall be called the spin loop director, is decoupled from the 12 outer spins, and hence its reorientation embodies the long-sought local zero-energy mode for the pyrochlore lattice.
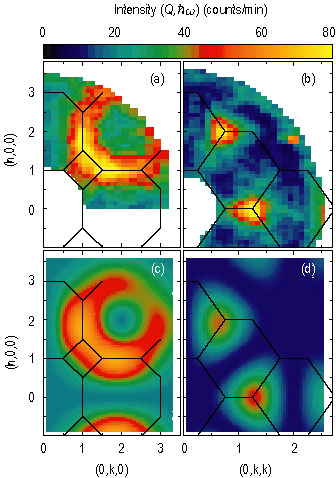
| Figure 2. (A) and (B): Color images of inelastic neutron scattering intensities from single crystals of zinc, cromium sub 2, oxygen sub 4, in the (h k 0) and (h k k) symmetry planes obtained at T = 15 K for h bar omega = 1 milli electron volt. The data are a measure of the dynamic form factor for self-organized nano-scale spin clusters in the material. (C) and (D): Color images of the square of the form factor calculated for antiferromagnetic hexagon spin loops averaged over the four hexagon orientations in the spinel lattice. The excellent agreement between model and data identifies the spin clusters as hexagonal spin loops. |
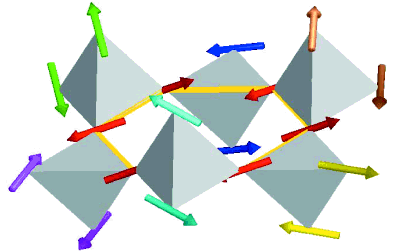
| Figure 3. Spin cluster surrounding a hexagon (shown in gold) in the pyrochlore lattice of Figure 1. |
Composite degrees of freedom are common in strongly interacting many body systems. Quarks form hadrons; hadrons form nuclei; nuclei plus electrons form atoms; atoms form molecules that in turn are the basis for complex biological functionality. Planets, stars, galaxies and galactic clusters are examples of clustering on grander length scales. However, to our knowledge, the emergence of a confined spin cluster degree of freedom has not previously been documented in a uniform gapless magnet. The discovery is important because magnets offer an opportunity not afforded by the aforementioned systems, namely, to monitor emergent structure in complex interacting systems with microscopic probes such as neutron scattering and N M R. The collapse of a geometrically frustrated magnet into a director protectorate could for example be a useful template for exploring aspects of protein folding (Refer to reference 2).
References
[1] P. G. Debenedetti et al., Nature 410, 259 (2001).
[2] P. G. Wolynes and W. A. Eaton, Physics World 12, 39 (1999).
[3] S.-H. Lee, C. Broholm, W. Ratcliff, G. Gasparovic, Q. Huang, T. H. Kim, and S.-W. Cheong, Nature, in press (2002).
[4] S.-H. Lee et al., Phys. Rev. Lett. 84, 3718 (2000).
[5] R. B. Laughlin and D. Pines, Proc. Natl. Acad. Sci. U.S.A. 97, 28 (2000).
Authors
S.-H. Lee, Q. Huang
NIST Center for Neutron Research
National Institute of Standards and Technology
Gaithersburg, MD 20899-8562
C. Broholm, G. Gasparovic
Department of Physics and Astronomy
The Johns Hopkins University
Baltimore, MD 21218
W. Ratcliff, S.-W. Cheong
Department of Physics and Astronomy
Rutgers University
Piscataway, NJ 08854
T. H. Kim
Francis Bitter Magnet Laboratory
Massachusetts Institute of Technology
Cambridge, MA 02139
Back to FY2002 HTML main page
Go to next article
To view all symbols correctly, please download Internet Explorer 6 or Netscape 7.1