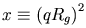TwoHomopolymerRPA

Alan Munter 08 JULY 1999

Calculates the form factor, P(q), for a system of two homopolymers in the random phase approximation(RPA).

Resolution smeared version is also provided.

Input Variables (default values):

Parameter	Variable	Value
0	Degree of Polymerization A	1000.0
1	Degree of Polymerization B	1000.0
2	Volume Fraction of Polymer A	0.2
3	Volume of a Segment of Polymer A(cm3/mol)	100.0
4	Volume of a Segment of Polymer B(cm3/mol)	100.0
5	Contrast A-B(Å-2)	2.0e-6
6	Length of a Segment of Polymer A(Å)	6.0
7	Length of a Segment of Polymer B(Å)	7.0
8	Interaction between Polymers A and B	0.0
9	Incoherent Background (cm-1)	0.0

The function calculated is:

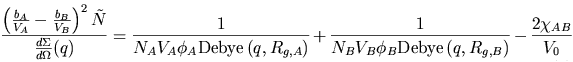
where , , ,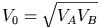

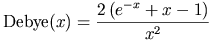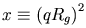
and with the following definitions:

The degree of polymerization in Parameter[0] and Parameter[1] is the number of base segments that are included in the polymer chains.

The Volume Fraction of Polymer B is calculated as (1 - Parameter[2]).

Typical segment lengths are less than 10 Å for polymers like polystyrene.

If the interaction parameter is made too large it will result in unphysical results since the RPA is no longer applicable for strongly interacting polymers.

The returned value is in units of [cm^-1] since it is scaled to the volume fractions of the polymers.

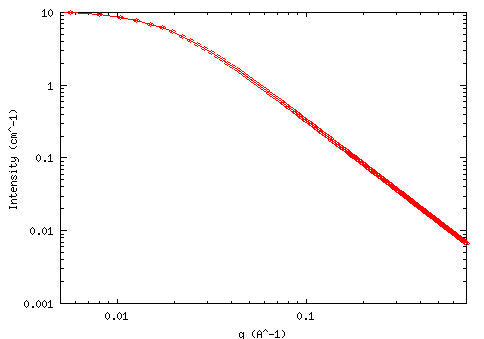
This example dataset is produced by calculating the TwoHomopolymerRPA using 300 data points, q_min = 0.001 Å^-1, q_max = 0.7 (Å^-1) and the above default parameter values.
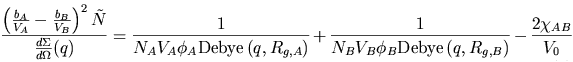
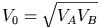
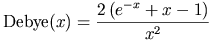