MODEL
PolyRectSphere
AUTHOR/MODIFICATION
Steve Kline 20 JAN 1999
Alan Munter 08 JULY 1999, converted to Java
APPROVED FOR DISTRIBUTION
DESCRIPTION
Calculates the form factor for a polydisperse population of spheres
with uniform scattering length density. The distribution of radii is
a rectangular (box) distribution. The form factor is normalized by
the average particle volume such that P(q) =
scale*<f*f>/Vol + bkg, where f is the single
particle scattering amplitude and the < > denote an average over
the size distribution.
Resolution smeared version is also provided.
VARIABLES
Input Variables (default values):
| Parameter | Variable | Value |
| 0 | Scale | 1.0 |
| 1 | Average Radius (Å) | 60.0 |
| 2 | Polydispersity (0-1) | 0.12 |
| 3 | Contrast (Å-2) | 3.0e-6 |
| 4 | Incoherent Background(cm-1) | 0.000 |
USAGE NOTES
The returned value is scaled to units of [cm-1],
absolute scale.
contrast = SLD (sphere) - SLD (solvent)
The (normalized) rectangular distribution is:
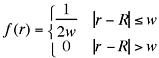
with the constraint that w <= R. Here R is the average
radius specified by parameter[1] above.
R is the mean of the distribution and w is the half-width.
The root mean square deviation is
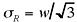 . The polydispersity,
. The polydispersity,
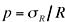 .
.
The form factor is normalized by the average volume, using
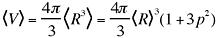 .
.
If the scale factor Parameter[0] is set equal to the particle
volume fraction, phi, the returned value is the scattered
intensity per unit volume, I(q) = phi*P(q).
However, no interparticle interference effects are included in this
calculation.
Parameter[0] (scale) and Parameter[3] (contrast) are multiplicative
factors in the model and are perfectly correlated. Only one of these
parameters should be left free during model fitting.
REFERENCE
Kotlarchyk, M.; Chen, S.-H. J. Chem. Phys., 1983,
79, 2461.
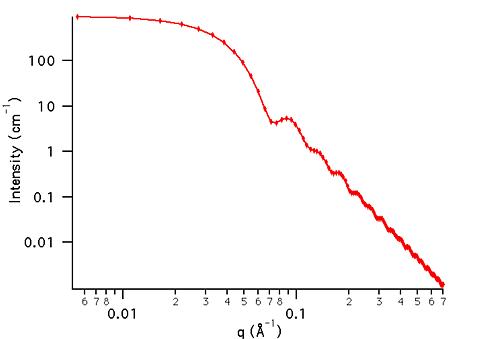
TEST DATASET
This example dataset is produced by calculating the PolyRectSphere
using 128 data points, qmin = 0.001 Å-1,
qmax = 0.7 Å-1 and the above default
parameter values.
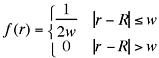
![]() . The polydispersity,
. The polydispersity,
![]() .
.![]() .
. 