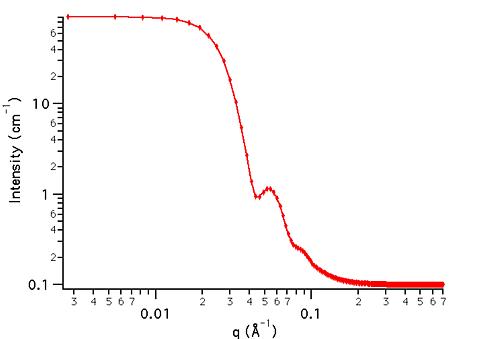
This example dataset is produced by calculating the PolyHardSphere using 256 data points, qmin = 0.001 Å-1, qmax = 0.7 Å-1 and the above default parameter values.
MODEL
PolyHardSphere
AUTHOR/MODIFICATION
Steve Kline 06 NOV 1998
Alan Munter 08 JULY 1999, converted to Java.
APPROVED FOR DISTRIBUTION
DESCRIPTION
This function calculates the scattered intensity for a population of polydisperse spheres, including hard sphere interactions between the particles. The calculation is an exact, multicomponent solution, using the Percus-Yevick closure. A Schulz distribution is used to describe the polydispersity of the diameter.
VARIABLES
Input Variables (default values):
| Parameter | Variable | Value |
|---|---|---|
| 0 | Radius (Å) | 100.0 |
| 1 | Polydispersity (0-1) | 0.12 |
| 2 | Volume Fraction (0-1) | 0.1 |
| 3 | Contrast (Å-2) | 2.0e-6 |
| 4 | incoherent Background(cm-1) | 0.000 |
USAGE NOTES
The returned value is the scattered intensity in absolute scale, units of [cm-1]. Since both the form factor and structure factor are included in this calculation, any other structure factor selected in the calculation will not be applied.
Polydispersity, p = s/R, where s2 is the variance of the distribution and R is the mean particle radius, Parameter[0]. For a more complete description of the Schulz distribution, see: J. Hayter in "Physics of Amphiphiles - Micelles, Vesicles and Microemulsions" V. DeGiorgio and M. Corti, Eds. (1983) p. 69.
Polydispersity, Parameter[1], is constrained during calculation to remain between its physical limits of 0 < p < 1. If a value larger than this is entered the value is quietly converted to 1.
Scattering contrast = SLD (sphere) - SLD (solvent).
Volume fraction and scattering contrast are correlated, and one or both should be held fixed during model fitting.
REFERENCE
Griffith, W. L.; Triolo, R.; Compere, A. L. Phys. Rev. A, 1987, 35, 2200.
TEST DATASET
This example dataset is produced by calculating the PolyHardSphere using 256 data points, qmin = 0.001 Å-1, qmax = 0.7 Å-1 and the above default parameter values.
