HollowCylinder

Steve Kline 20 JAN 1999

Alan Munter 08 JUL 1999, converted to Java

Alan Munter 20 OCT 2000, corrected a calculation error.

Calculates the form factor for a monodisperse, hollow, right circular cylinder (or a tube). The inside and outside of the tube have the same scattering length density and the tube itself is of uniform SLD. The form factor is normalized by the tube material volume ONLY such that P(q) = scale*<f*f>/Vol + bkg, where f is the scattering amplitude and the < > denote an average over all possible orientations of the cylinder.

Resolution smeared version is also provided.

Input Variables (default values):

Parameter	Variable	Value
0	Scale	1.0
1	Core Radius (Å)	20.0
2	Shell Radius (Å)	30.0
3	Length (Å)	400.0
4	Contrast (Å-2)	3.0e-6
5	Incoherent Background (cm-1)	0.0

The function calculated is:

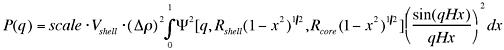
where J₁ is the first order Bessel function. The integral over x is the orientaional average and the returned form factor is scaled to units of [cm^-1].

contrast = SLD (shell) - SLD (solvent)

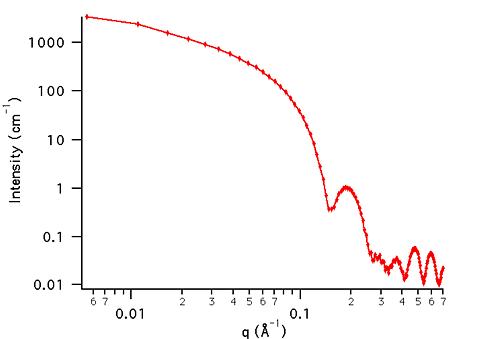
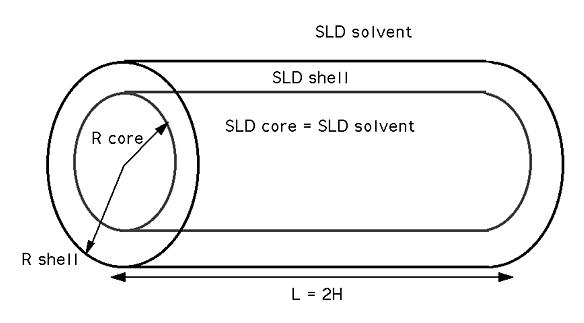
The shell thickness is uniform over the cylinder radius. There is no material covering the ends of the tube. This mean that for the default case above, the total diameter of the cylinder is 2*30 = 60 Å and that the total length is 400 Å. The 40 Å diameter core is assumed to be the same scattering length density as the solvent, giving no contribution to the scattered intensity.

The form factor is normalized to the volume of material comprising the shell such that . Note that this is different than the total excluded volume of the hollow cylinder, which is .

Parameter[0] (scale) and Parameter[4] (contrast) are multiplicative factors in the model and are perfectly correlated. Only one of these parameters should be left free during model fitting.

The user should ensure that the shell radius is always larger than the core radius.

If the scale factor Parameter[0] is set equal to the particle volume fraction, phi, the returned value is the scattered intensity per unit volume, I(q) = phi*P(q). However, no interparticle interference effects are included in this calculation.

Feigin, L. A, and D. I. Svergun, "Structure Analysis by Small-Angle X-Ray and Neutron Scattering", Plenum Press, New York, (1987).

This example dataset is produced by calculating the HollowCylinder using 128 data points, q_min = 0.001 Å^-1, q_max = 0.7 Å^-1 and the above default parameter values.