MODEL
Debye-Anderson-Brumberger (DAB)
AUTHOR/MODIFICATION
Charlie Glinka 05 DEC 1998
Alan Munter 08 JULY 1999, converted to Java
APPROVED FOR DISTRIBUTION
DESCRIPTION
Calculates the scattering from a randomly distributed (i.e.
nonparticulate), two-phase system based on the Debye-Anderson-Brumberger
(DAB) model for such systems. The two-phase system is characterized
by a single length scale, the correlation length, which is a measure
of the average spacing between regions of phase 1 and phase 2. The
model also assumes smooth interfaces between the phases and hence
exhibits Porod behavior (I ~ Q-4) at large Q (Q*correlation
length >> 1). The macroscopic scattering cross-section in the
DBA model is given by
dS/dW = A/(1 + (q*a)^2)^2
where a is the correlation length in Å.
Resolution smeared version is also provided.
VARIABLES
Input Variables (default values):
| Parameter | Variable | Value |
| 0 | Scale | 10.0 |
| 1 | Radius (Å) | 40.0 |
| 2 | Incoherent Background (cm-1) | 0.0 |
USAGE NOTES
The returned value is in units of [cm-1].
The scale factor, A or Parameter[0], is treated as an independent
fitting parameter, but is, in the DBA model, related to the volume
fractions of the two phases, f1 and f2, their contrast,
(sld_1 - sld_2)2, and the correlation length, a, as follows:
A = 8*p*a3*contrast*f1*f2
The surface, S, to volume, V, ratio for the system is given by
S/V = 4*f1*f2/ a
REFERENCES
Debye, P., Anderson, R., Brumberger, H., "Scattering by an
Inhomogeneous Solid. II. The Correlation Function and Its Application,"
J. Appl. Phys. 28 (6), 679 (1957).
Debye, P., Bueche, A. M., "Scattering by an Inhomogeneous Solid,"
J. Appl. Phys. 20, 518 (1949).
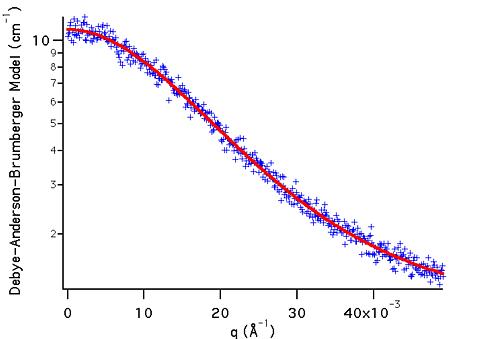
TEST DATASET
This example dataset is produced by multiplying the values generated
by the Model DAB (using the default parameter values given above) by
(1 + gnoise(.05)) to simulate real data with 5% gaussian noise. The
q-range has been restricted to (0.001,0.05) Å-1.