Since the bulk of the present work deals with neutron reflectometry,
the technique will be developed below in greater detail than any of
the other analysis techniques.
Neutron reflectometry is a technique in which neutrons at thermal energies
are used to
probe the near surface structure of material systems. In neutron
reflectometry,
neutrons are incident on a surface at a grazing angle of less than 3![]() .
At these small angles, the potential for scattering can be approximated
by a continuous
value, as will be shown later, and this value is called the scattering
length density
(SLD) usually denoted in equations as
.
At these small angles, the potential for scattering can be approximated
by a continuous
value, as will be shown later, and this value is called the scattering
length density
(SLD) usually denoted in equations as ![]() .
It is a product of the scattering length of each isotope and
that isotope's number density.
.
It is a product of the scattering length of each isotope and
that isotope's number density.
For neutrons of thermal energies, the very small angles of incidence can be sufficient to cause the neutrons to be totally reflected from the surface. The position of this transition to total reflection yields information about the average SLD of the material. The calculation of this total reflection (critical) angle will be discussed below. The reflectivity away from the total reflection angle holds information about the change in scattering length density with depth. It can be analyzed to determine a film's total thickness, material composition, periodicity, and even roughness.
The geometry of a typical reflectometry experiment is shown in Fig. 1. The data are measured as
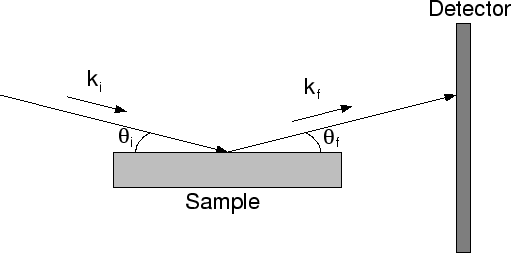 |
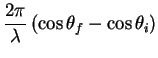 |
(1) | ||
 |
(2) |
When
![]() ,
, ![]() , and the scattering is called
specular. This is the condition that is used to determine the structure of the
material in the
, and the scattering is called
specular. This is the condition that is used to determine the structure of the
material in the ![]() direction, perpendicular to the surface. When
dealing with specular reflectivities the data are usually presented as
a function of
direction, perpendicular to the surface. When
dealing with specular reflectivities the data are usually presented as
a function of ![]() .
.
The geometry that was assumed in the discussion above and shown
in Fig. 1 is the forward scattering geometry.
In this geometry, the direction perpendicular to the plane of
reflection, the ![]() -direction, is neglected. The slits which
collimate the beam of neutrons are very wide in this direction (>
1 cm), so any measurements are assumed to be integrated over the out-of-plane
direction. For this reason, all of the equations presented here will have the
-direction, is neglected. The slits which
collimate the beam of neutrons are very wide in this direction (>
1 cm), so any measurements are assumed to be integrated over the out-of-plane
direction. For this reason, all of the equations presented here will have the
![]() and
and ![]() dependence eliminated or integrated over.
dependence eliminated or integrated over.
Most reflectivity curves have three basic features.
The first is the critical wave-vector transfer ![]() . Neutrons are
totally reflected for values of
. Neutrons are
totally reflected for values of ![]() below
below ![]() .
For a uniform film,
.
For a uniform film, ![]() is given by
is given by
A second feature of reflectivity profiles is the decrease in intensity (or
reflectivity) with ![]() which, for a smooth sample, becomes
proportional to
which, for a smooth sample, becomes
proportional to ![]() as
as ![]() increases.
A thin film can also show oscillations, the third feature, around this
continuously
decreasing reflectivity; the result of an interference effect between the
air/film and film/substrate interfaces. The amplitude of these
thickness oscillations is proportional to the difference in SLD
between the thin film and the substrate, often referred to as the SLD
contrast.
An estimate of the film's thickness is given by
increases.
A thin film can also show oscillations, the third feature, around this
continuously
decreasing reflectivity; the result of an interference effect between the
air/film and film/substrate interfaces. The amplitude of these
thickness oscillations is proportional to the difference in SLD
between the thin film and the substrate, often referred to as the SLD
contrast.
An estimate of the film's thickness is given by
![]() , where
, where ![]() is the oscillation period.
is the oscillation period.
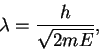 |
(5) |
| (6) |
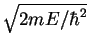 ,
,
The 3-D steady state Schrödinger equation in three dimensions is given
by
| (8) |
Since in specular
reflection we are only concerned with the structure of the medium in the ![]() direction, perpendicular to the surface, and since off-specular scattering
requires a special treatment, we will assume that
direction, perpendicular to the surface, and since off-specular scattering
requires a special treatment, we will assume that
![]() is a function of
is a function of
![]() only. This assumption is appropriate to the presentation of the basic
development of the different equations, but it is not completely appropriate
when calculations are made for real surfaces which usually have some kind of
roughness. The only assumption that must be made about the SLD in the
only. This assumption is appropriate to the presentation of the basic
development of the different equations, but it is not completely appropriate
when calculations are made for real surfaces which usually have some kind of
roughness. The only assumption that must be made about the SLD in the ![]() direction is that it has the limiting values
direction is that it has the limiting values
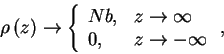 |
(9) |
| (10) |
where
![]() satisfies the equation
satisfies the equation
Since
![]() as
as
![]() , the above equation
is just the equation for a wave in free space above the sample
, the above equation
is just the equation for a wave in free space above the sample
where ![]() is the reflectance of the wave from the surface. If the wave
equation is determined above the surface of the sample it will have the form
is the reflectance of the wave from the surface. If the wave
equation is determined above the surface of the sample it will have the form
| (13) |
The square modulus of the coefficient ![]() , the complex amplitude of the
reflected wave, is called the reflectivity, and it is this quantity that is
measured. For specular reflectivity, since
, the complex amplitude of the
reflected wave, is called the reflectivity, and it is this quantity that is
measured. For specular reflectivity, since ![]() and
and ![]() are
conserved, the momentum transfer vector has only one component:
are
conserved, the momentum transfer vector has only one component:
![]() .
.
In order to begin a calculation of the reflectance, ![]() , we first begin by
setting the scattering length density equal to
, we first begin by
setting the scattering length density equal to
If we define an operator ![]() such that
such that
| (15) |
This Green's function is a wave traveling from the point ![]() ,
and Eq. 16 can be rewritten as an integral equation using this
Green's function and the previous definitions
,
and Eq. 16 can be rewritten as an integral equation using this
Green's function and the previous definitions
The solution to Eq. 17 has the asymptotic form
When Eq. 20 and Eq. 21 are substituted into
Eq. 19 is can be seen just by inspection that the equation has
the form of Eq. 12 and that the reflection coefficient, ![]() ,
can be expressed as
,
can be expressed as
Also called the first Born approximation or just the Born approximation,
this approximation assumes that the entire scattering event is just a
perturbation of the incoming beam so we set[1]
| (23) |
| (25) |
When Eq. 24 and this Green's function are substituted into
Eq. 22 the reflected amplitude becomes
No assumption has been made about the form of the incoming wave yet in
Eq. 26, so
the above equation is still technically an exact result.
For the plane wave Born
approximation, we assume
![]() and the reflected
amplitude is
and the reflected
amplitude is
| (27) |
The DWBA assumes that the unperturbed wave is a wave reflected
from a completely smooth surface so we set[1]
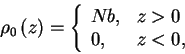 |
(28) |
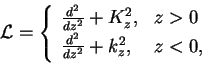 |
(29) |
We know that the solution of Eq. 17 has the form of a
wave that is partially reflected and partially refracted at ![]() :
:
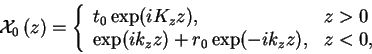 |
(30) |
![\begin{displaymath}
\ensuremath{G \left( z \mid z^{\prime} \right)}= \frac{2\pi}...
...ime}})], & \ensuremath{z^{\prime}}< 0 < z .
\end{array}\right.
\end{displaymath}](img142.gif) |
(31) |
| (32) |
![$\displaystyle r_0 + \frac{2\pi}{ik_z} \int_{0}^{\infty} \{ \left[
\exp (-ik_z z) + r_0 \exp(ik_z z) \right]^{2} \ensuremath{\rho_{1} \left( {-z} \right)}$](img146.gif) |
(33) | ||
| (34) |
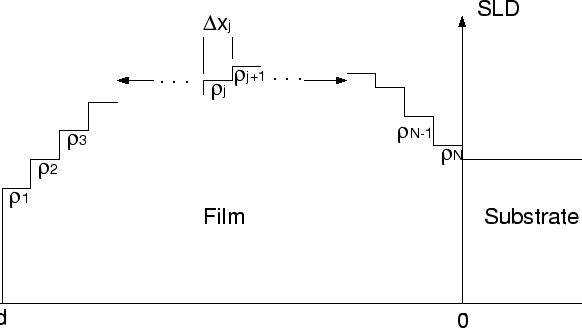
The final method of calculating reflectivities presented
here is an iteratively exact method called Parratt's recursion
relation[2].
The basic principle for this relation is very simple. The model scattering
length density profile is broken up into a series of layers as shown in
Fig. 2. The ![]() layer has a thickness
layer has a thickness ![]() and the
and the ![]() component of the wave number
component of the wave number
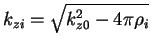 , where
, where ![]() is the incident wave number in air in the
is the incident wave number in air in the ![]()
 |
| (35) |
Each of these waves are originating from a depth ![]() in
the medium. The first derivative of the wave in each layer is given by
in
the medium. The first derivative of the wave in each layer is given by
| (36) |
| (37) | |||
| (38) |
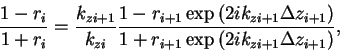 |
(41) |
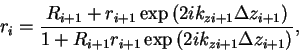 |
(42) |
This document was generated using the LaTeX2HTML translator Version 99.1 release (March 30, 1999)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -white NR_article
The translation was initiated by on 2000-04-20