|
|
|
| Home | Live Data | Instruments | CHRNS | Proposals |
How thick should my sample be?
Cautionary remarks
The most common answer to the question "How thick should my sample be?", or more generally "What should be the dimensions of my sample?", is that the sample should be a "10% scatterer", which presumably means that 10% of the neutrons that enter the sample are scattered at least once (or does it means that 10% of the neutrons are scattered once and then leave without being absorbed or scattered again?) The argument is that a "10%" scatterer scatters roughly 10% of the scattered neutrons a second time (and ~10% of those neutrons yet again), and that this amount of multiple scattering is in some sense acceptable.The fact that a sample is a "10% scatterer" does not necessarily imply that ~10% of the scattered neutrons are scattered again before they exit the sample. For example, Wuttke (Physica B 292, 194 (2000)) has shown that a thin annular sample whose transmission is 96% for a tightly collimated beam, and ~94% for a beam that fully illuminates the sample, scatters ~10% of the scattered neutrons a second time. This implies that a "10% scatterer", meaning a sample with little absorption and a transmission of about 90% (depending how it is measured), scatters something like 15-25% of the neutrons a second time.
An experimentalist sometimes has to decide the dimensions of his or her sample using a calculated value for the transmission. This implies that the macroscopic scattering and absorption cross sections are known. The number density can generally be calculated quite well, and the microscopic cross sections are generally obtained from a compilation such as that of Sears in Neutron News 3 (3), 26 (1992). This approach can be quite misleading, especially for hydrogenous materials. This is discussed below, under the heading Scattering cross sections .
Calculating the scattering probability given the dimensions of a sample
Given the proposed geometry (we shall consider slabs, cylinders and annular samples), and the relevant macroscopic scattering and absorption cross sections ,and
respectively, the scattering probability , S, can be calculated. Note that S is the probability of scattering at least once (followed by escape, absorption or additional scattering); in general it is an overestimate of the total scattering probability.
For a slab sample of thickness, t, whose normal is at an angle
to the beam,
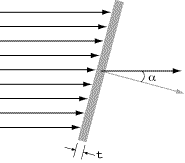
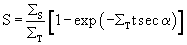
For a cylindrical sample of radius R, with axis normal to the beam,
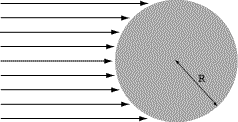
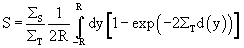
where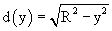 
For an annular sample with inner and outer radii
and
respectively (annular thickness
), whose axis is normal to the beam,
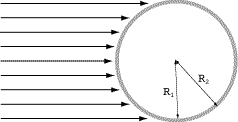
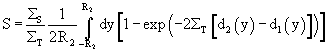
where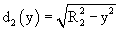 
and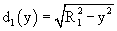 
if ,
otherwise .
Calculating the dimensions of a sample given its scattering probability
Slab sample
For a slab sample normal to the beam, the value t can be obtained directly from the the single scattering probability expression:
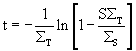
There is no solution if
.
Annular Sample
For the general case there is no analytical solution so the integral must be calculated numerically. An approximate solution (which is only valid if
) is based on the approximate result
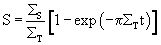
which yields
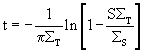
Again there is no solution if
Cylindrical Sample
In this case there is again no analytical solution. The integral can be calculated numerically as a function of the dimensionless magnitude,
R.
Scattering cross sections
The macroscopic total scattering cross section;
The macroscopic bound atom scattering cross section
with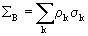 
,
and
.
In these expressions,
is the number density of atoms of element k,
is the total (coherent plus incoherent) bound atom scattering cross section of element k,
is the number of atoms of element k per scattering unit,
is the mass density,
is Avogadro's number, M is the mass ("molecular weight") of a scattering unit, and
is the atomic mass of element k.
The macroscopic total scattering cross section
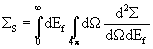
where
is the macroscopic differential cross section for scattering into solid angle
and scattered energy
.
The need to distinguish between
(1 meV) is ~240 b/molecule. On the other hand
The macroscopic total cross section
.
Report errors or make inquiries to Inma Peral, <inma@nist.gov>
Last modified 02-August-2007 by website owner: NCNR (attn: )