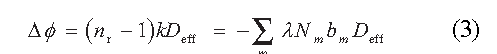Measurement of Deuterium Scattering Length
A recent high precision measurement
of the scattering length, b, of
deuterium gas has been performed using
neutron interferometry at the NIST Neutron
Interferometer and Optics Facility [ 1, 2 ]. Accurate
measurement of the scattering length is important to
the fundamental nature of how a neutron scatters from
an atom. This scattering length depends on the nature of
the nuclear potential, and, therefore, the prediction of this
value is an important test for models of the nuclear
potential. Currently only few nucleon systems can be
accurately modeled, and measurements of scattering
lengths of light nuclei are considered to be the most
interesting. To date the most accurate methods to measure
the scattering length have been neutron optical methods,
and prior to this work the most accurate determination of
the scattering length of deuterium has been that of gravity
reflectometry. These neutron optical methods measure the
bound coherent scattering length, b, by accurately determining
the index of refraction, n, given by,
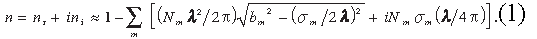
In Equation ( 1 ), m is the elemental species ( important
when correcting for contaminants ); b is the local mean
forward coherent scattering length averaged over the two
spin dependent free scattering channels
where 2S + 1an d
( for S = total spin = [ 1/2 or 3/2 ] ) are the free
doublet and quartet scattering lengths; mn is the neutron
mass and md is the deuteron atomic
mass;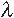 is the neutron deBroglie
wavelength;
is the neutron deBroglie
wavelength; 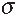 is the total cross
section made up of the scattering and
absorption cross sections; nr is the
real part of the index of refraction;
and N is the atom density of the
material. For all elements the real part
of n is nearly unity: the magnitude of
( nr - 1 ) for typical neutron-nucleus
potentials is approximately 1 X 10-5.
is the total cross
section made up of the scattering and
absorption cross sections; nr is the
real part of the index of refraction;
and N is the atom density of the
material. For all elements the real part
of n is nearly unity: the magnitude of
( nr - 1 ) for typical neutron-nucleus
potentials is approximately 1 X 10-5.
The imaginary part of Equation ( 1 ) accounts
for the attenuation of the wave
amplitude due to scattering and absorption. Although such
inelastic processes do not contribute to the interference of
the amplitudes that travel on the two different paths
through the interferometer since they make the path
distinguishable in principle, they appear in the expression
for the forward scattering amplitude as a result of the
optical theorem. The interferometer efficiently filters out
such inelastic processes that occur in the sample and in the
Si interferometer blades.
Neutron interferometry is mainly sensitive to the
real part of the refractive index by measuring the phase
shift of a sample placed on one of two indistinguishable
paths in the silicon neutron interferometer [ 3 ]. This phase
shift can be written as
( 3 )
where De f f stands for the effective thickness of the medium
along the direction of wave propagation. This phase shift
can be very large; thus the neutron interferometric method
is very sensitive to the index of refraction. Here we
present the results of a measurement of the phase shift of a
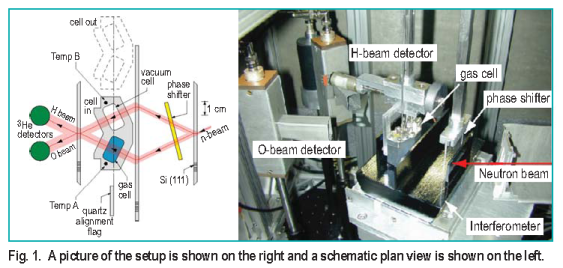
1 cm thick sample of D2 gas. The experimental setup for
this measurement is shown in Figure 1. The phase shift data
converted to scattering length by inverting Equation ( 3 ) are
shown plotted in Figure 2.
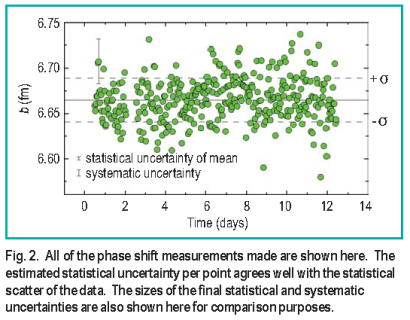
Finally, averaging all values in
Figure 2 and combining the statistical and systematic uncertainties,
we obtain the value for the scattering length
bn d = ( 6.665 ± 0.004 ) fm, which is plotted relative to
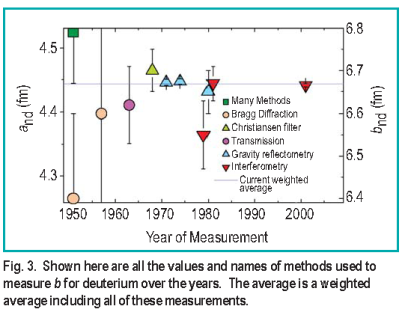
previous measurements of the scattering length in Figure 3.
The new world average is then bn d = ( 6.669 ± 0.003 ) fm,
which is slightly lower than the previous world average of
bn d = ( 6.673 ± 0.0045 ) fm.
This measurement has improved on the uncertainty
reported by previous interferometric measurements by
more than a factor of 10, and by nearly a factor of two
over the previous results from gravity reflectometry. Such
precision measurements of the scattering length are
important for various theories dealing with 3 nucleon
forces ( 3NF ). Looking back at Equation ( 2 ), the quartet
scattering length, which is a long-range nuclear interaction,
can be calculated accurately from nucleon-nucleon
potentials and is insensitive to 3NF effects that are currently
used to calculate the shorter range doublet scattering
length. Because the effective range function in the quartet
spin channel is a smooth function of energy, the quartet
scattering can be accurately extracted from an energy
dependent phase shift analysis, so that experimental
measurement of the bound coherent scattering length and
theoretical calculation of the quartet scattering length allow
the doublet scattering length to be extracted and compared
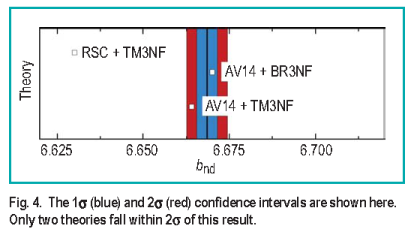
to calculation using 3NF models. Only one of the scattering
length calculations reported previous to this result falls
within the ( ± 1 )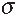 confidence band of this measurement
shown in Figure 4.
confidence band of this measurement
shown in Figure 4.
Future experiments will be able to lower the combined
systematic and statistical uncertainty by as much as
a factor of 5. This would allow one to measure higher
order effects due to molecular binding in H2 and D2. Other
elements such as ³He and ³H2 could also be measured with
lower uncertainties than those currently in the open
literature.
References
[1] T. C. Black, P. R. Huffman, D. L. Jacobson, W. M. Snow, K. Schoen,
M. Arif, H. Kaiser, S. K. Lamoreaux, and S. A. Werner
Phys. Rev. Lett. 90, 192502 (2003).
[2] K. Schoen, D. L. Jacobson, M. Arif, P. R. Huffman, T. C. Black, W.
M. Snow, S. K. Lamoreaux, H. Kaiser, and S. A. Werner
Phys. Rev. C 67, 044005 (2003).
[3] H. Rauch, S. Werner, Neutron Interferometry: Lessons in Experimental
Quantum Mechanics, Oxford University Press, 2000.
P. R. Huffman, D. L. Jacobson and M. Arif
Physics Laboratory Ionizing Radiation Division
National Institute of Standards and Technology, Gaithersburg, MD 20899-8461
S. A. Werner
Physics Laboratory Ionizing Radiation Division
National Institute of Standards and Technology, Gaithersburg, MD 20899-8461
and
University of Missouri-Columbia, Columbia, MO 65211
K. Schoen and H. Kaiser
University of Missouri-Columbia, Columbia, MO 65211
T. C. Black
University of North Carolina at Wilmington, Wilmington, NC 28403-3297
W. M. Snow
Indiana University/IUCF, Bloomington, IN 47408
and
S. K. Lamoreaux
Los Alamos National Laboratory
Los Alamos, NM 87545
Back to FY2003 HTML main page
Go to previous article
Go to next article
To view all symbols correctly, please download
Internet Explorer 6 or Netscape 7.1
Last modified 11-March-2004 by website owner: NCNR (attn: )
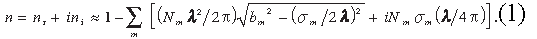
![b equals the quanity m sub n plus m sub d all over m sub d, times, [ 1/3 squared times pre-superscript two a sub n d, plus 2/3 times pre-superscript 4 a sub n d ]](RH3_EQ2.png)
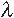 is the neutron deBroglie
wavelength;
is the neutron deBroglie
wavelength;  is the total cross
section made up of the scattering and
absorption cross sections; nr is the
real part of the index of refraction;
and N is the atom density of the
material. For all elements the real part
of n is nearly unity: the magnitude of
( nr - 1 ) for typical neutron-nucleus
potentials is approximately 1 X 10-5.
is the total cross
section made up of the scattering and
absorption cross sections; nr is the
real part of the index of refraction;
and N is the atom density of the
material. For all elements the real part
of n is nearly unity: the magnitude of
( nr - 1 ) for typical neutron-nucleus
potentials is approximately 1 X 10-5.