The transition metal oxides have been the source of many fascinating physical phenomena such as high Tc superconductivity, colossal magnetoresistance, and orbiton physics [ 1 ]. These surprising and diverse physical properties arise from strong correlation effects in the 3d bands. Most theoretical attempts to understand such systems are based on the Hubbard model. Here we report that for high symmetry transition metal oxides with threefold t2g bands, this model possesses several novel hidden symmetries with many surprising consequences on the ground state properties [ 2, 3 ].
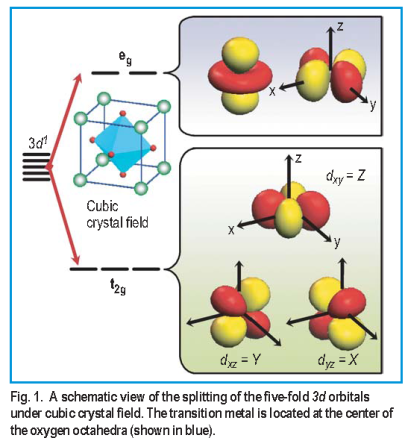
We consider cubic 3d1 perovskites ( i.e., ABO3 )
where the five initially degenerate 3d states are split into a
two-fold eg manifold and a lower-energy threefold t2g
manifold with wavefunctions dyz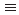 X, dxz
X, dxz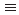 Y, and dxy
Y, and dxy 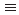 Z ( see Figure 1 ). Keeping only the t2g states, we base our
discussion on the following generic three-band Hubbard Hamiltonian:
Z ( see Figure 1 ). Keeping only the t2g states, we base our
discussion on the following generic three-band Hubbard Hamiltonian:
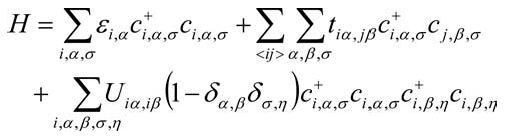
Here 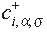 creates a t2g electron ( or hole ) on the ith
ion in the
creates a t2g electron ( or hole ) on the ith
ion in the 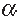 spatial orbital ( i.e.,
spatial orbital ( i.e.,
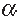 = X, Y or Z ) with spin
= X, Y or Z ) with spin 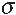 ,
and
,
and 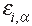 is the on-site energy of the orbital at site i of a
simple cubic lattice.
is the on-site energy of the orbital at site i of a
simple cubic lattice. 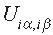 is the on-site Coulomb repulsion
between orbitals
is the on-site Coulomb repulsion
between orbitals 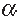 and
and 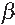 at site i .
at site i .
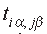 is the effective
hopping parameter from the
is the effective
hopping parameter from the 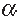 orbital at site i to the
orbital at site i to the 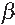 orbital at its nearest neighbour site j.
orbital at its nearest neighbour site j.
As shown in Figure 2, for cubic perovskites where the
metal-oxygen-metal ( M-O-M ) bond is linear, the hopping
parameter 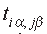 is diagonal in the orbital indices
is diagonal in the orbital indices
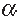 and
and  .
This suggests that the total number of electrons in each
orbital is a good quantum number. Furthermore
.
This suggests that the total number of electrons in each
orbital is a good quantum number. Furthermore 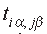 is
zero along the “inactive” axis perpendicular to the orbital
plane
is
zero along the “inactive” axis perpendicular to the orbital
plane 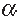 , due to symmetry ( Figure 2 ). In other words an
, due to symmetry ( Figure 2 ). In other words an
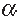 -electron can only hop in
-electron can only hop in 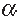 -plane. Thus, for the nth plane
perpendicular to the
-plane. Thus, for the nth plane
perpendicular to the 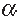 -axis, the total number Nn alpha of
electrons in the
-axis, the total number Nn alpha of
electrons in the 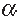 -orbital is conserved, i.e., it is a good
quantum number. Hence, one can consider the three
dimensional lattice as a superposition of interpenetrating
planes perpendicular to the x, y, and z-directions, each
having a constant number of X, Y, and Z electrons,
respectively, which are good quantum numbers ( see
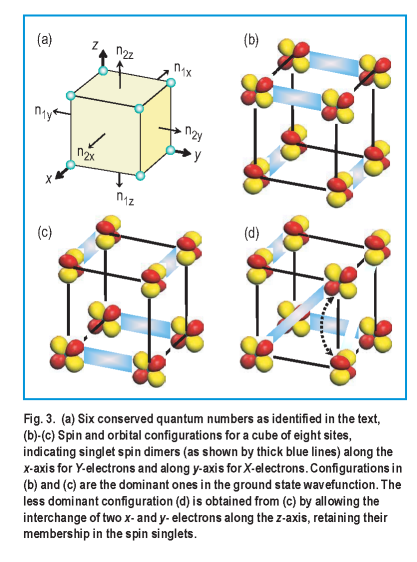
Figure 3 ( a ) ).
-orbital is conserved, i.e., it is a good
quantum number. Hence, one can consider the three
dimensional lattice as a superposition of interpenetrating
planes perpendicular to the x, y, and z-directions, each
having a constant number of X, Y, and Z electrons,
respectively, which are good quantum numbers ( see
Figure 3 ( a ) ).
In Reference [ 3 ] we also show that the global rotation of
the spins of  -orbital electrons in any given plane perpendicular
to the
-orbital electrons in any given plane perpendicular
to the  -axis leaves the Hubbard Hamiltonian given
in Equation ( 1 ) invariant. As a consequence of this rotational
symmetry, one may conclude that both the Hubbard model
and its 2nd order perturbation at order of t2/U, the Kugel-
Khomskii ( KK) Hamiltonian, cannot support any long range
spin order: if one assumes long-range spin order, the spins
associated with
-axis leaves the Hubbard Hamiltonian given
in Equation ( 1 ) invariant. As a consequence of this rotational
symmetry, one may conclude that both the Hubbard model
and its 2nd order perturbation at order of t2/U, the Kugel-
Khomskii ( KK) Hamiltonian, cannot support any long range
spin order: if one assumes long-range spin order, the spins
associated with 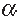 -orbitals within any given plane can be
rotated at zero cost in energy, thereby destroying the
supposed correlations among planes and/or among orbitals,
and therefore the long-range order [ 2, 3 ]. The crucial
conclusion here is that any credible theory of spin-ordering
in these systems cannot be based solely on the KK Hamiltonian,
as currently done in the literature.
-orbitals within any given plane can be
rotated at zero cost in energy, thereby destroying the
supposed correlations among planes and/or among orbitals,
and therefore the long-range order [ 2, 3 ]. The crucial
conclusion here is that any credible theory of spin-ordering
in these systems cannot be based solely on the KK Hamiltonian,
as currently done in the literature.
The hidden symmetries discussed here are very useful in simplifying the exact numerical studies of small clusters. For example, to treat the simpler KK Hamiltonian for a cube of eight sites even using the conservation of the total spin ( a widely used symmetry ) requires the diagonalization of a matrix of dimensionality on the order of ˝ million. Using the conservation laws applied to each face of the cube (see Figure 3 ( a ) ), there is an astonishing numeri- cal simplification. The ground state can be found from a Hamiltonian matrix within a manifold of just 16 states!! As seen in Figure 3 ( b - d ), these states are all products of four dimer states in each of which two electrons are paired into a spin zero singlet state. In this model a very unusual phenomenon occurs: when the electrons hop from site to site along active axes, they retain their membership in the singlet they started in. An example of this transformation is seen by comparing Figures 3 ( c ) and 3 ( d ): pairs of electrons are tied together, as if by quantum mechanical rubber bands!
In conclusion, we uncovered several novel symmetries of the Hubbard model for orthogonal t2g systems. Using these symmetries, we rigorously showed that both the original Hubbard Hamiltonian [ 2 ] and the KK effective Hamiltonian [ 1 ] ( without spin-orbit interactions ) do not permit the development of long-range spin order in a three dimensional orthogonal lattice at nonzero temperature. It is important to take proper account of the symmetries identified here and to recognize that the observed longrange spin order can only be explained with the Hubbard or KK Hamiltonian providing suitable symmetry breaking terms are included. Such perturbations therefore play a crucial role in determining the observed behavior of these transition metal oxides. We hope that these results will inspire experimentalists to synthesize new t2g transition metal oxides with tetragonal or higher symmetry. Such systems would have quite striking and anomalous properties.
References:
[1] Y. Tokura and N. Nagaosa, Science 288, 462 (2000) and references therein.
[2] A. B. Harris, T. Yildirim, A. Aharony, O. Entin-Wohlman, and I. Ya. Korenblit, Phys. Rev. Lett. (in press, 2003)(cond-mat/0303219).
[3] A. B. Harris, T. Yildirim, O. Entin-Wohlman, and A. Aharony, Phys. Rev. B (cond-mat/0307515).
T. Yildirim
NIST Center for Neutron Research
National Institute of Standards and Technology
Gaithersburg, MD 20899
A. B. Harris
University of Pennsylvania
Philadelphia, PA 19104
A. Aharony, O. Entin-Wohlman, and I. Ya. Korenblit
Tel Aviv University
Tel Aviv 69978, Israel