Spinels and pyrochlores are two of the most important crystal structures that are known to exhibit geometric magnetic frustration. In these materials there are three-dimensional networks of corner-sharing tetrahedra, a structural arrangement that leads to a high degree of magnetic frustration if the dominant nearest-neighbor interactions are antiferromagnetic. One interesting question that has not, to our knowledge, been addressed experimentally concerns whether half-integral spins exhibit fundamentally different behavior than integral spins in frustrated lattices. In order to address this issue we have been systematically investigating the magnetic and structural properties of spinels in which integer or halfinteger- spin transition metal ions are located on the Bsublattice. In this report we describe the results [ 1 ] for an integer-spin ( S = 1 ) frustrated magnet GeNi₂O₄.

GeNi₂O₄ is a normal spinel with the Ni^{2 +} ions on the magnetically frustrated B-sites and the non-magnetic Ge^{4 +} ions on the A-sites. GeNi₂O₄ becomes antiferromagnetic below a Néel temperature of T_N 12 K. The crystal structure of GeNi₂O₄ has been refined, based upon neutron powder diffraction data from BT-1, in the cubic space group Fd3m at all temperatures. The structural refinements clearly demonstrate that there is no more than 1 % cation inversion ( interchange of Ge^{4 +} and Ni^{2 +} ions between A and B sites ), since Ge and Ni have very different neutron scattering lengths. This information cannot be obtained from x-ray diffraction due to the similar x-ray scattering strengths ( atomic numbers ) of Ge and Ni. In addition, we have verified that GeNi₂O₄ remains cubic below T_N using very high-resolution synchrotron x-ray powder diffraction at the Advanced Photon Source [ 1 ].

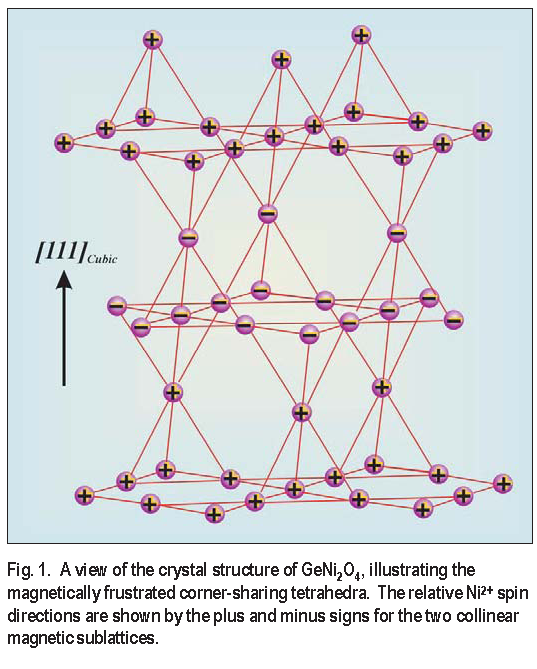
In Figure 1 we show the crystal structure of GeNi₂O₄, with the relative spin orientations of the Ni^{2 +} ions illustrated by plus and minus signs. The low temperature magnetic structure is a simple two-sublattice collinear structure in which the Ni^{2 +} spins are aligned in ferromagnetic ( 111 ) planes, and the spin direction of the ( 111 ) planes alternates along the [ 111 ] direction [ 2 ]. Assuming this magnetic structure, we obtain a good fit to the magnetic peak intensities in our low temperature ( T = 1.4 K ) neutron diffraction pattern.

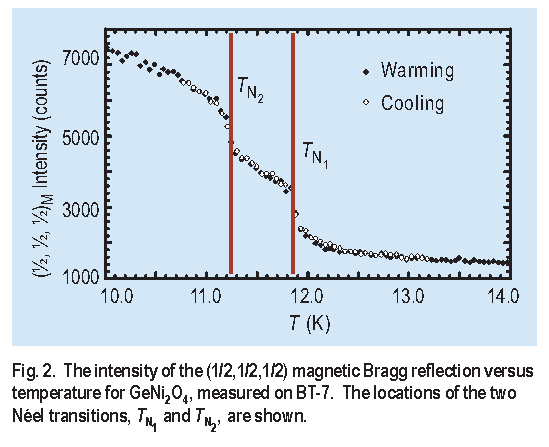
GeNi₂O₄ exhibits a surprising property, illustrated in Figure 2 where we plot the intensity of the magnetic ( ½, ½, ½ ) Bragg reflection as a function of temperature. The Néel transition in GeNi₂O₄ clearly consists of two distinct transitions, the first located at 12.13 K and the second at 11.46 K. Such double Néel transitions have been observed in one-dimensional frustrated antiferromagnets [ 3 ], such as the chain Haldane magnet CsNiCl₃, but this is the first observation, to our knowledge, of such a transition in a three-dimensional frustrated magnet. The small splitting of the Néel transition shows that the Ni^{2 +} ions in GeNi₂O₄ have very little magnetic anisotropy, and should thus be in the Heisenberg universality class.

The observation that GeNi₂O₄ remains cubic below T_N is in marked contrast with results for the transition metal oxide spinel ZnCr₂O⁴ [ 4 ]. ZnCr₂O₄ undergoes a cubic-tetragonal structural phase transition at T_N. Such structural transitions have been described [ 5, 6 ] as threedimensional analogs of the spin-Peierls transitions that occur in S = 1/2 one-dimensional antiferromagnets.

Furthermore, we have observed [ 1 ] the appearance of tetragonal distortions in two other spinels, GeCo₂O₄ ( S = 3/2, effective spin 1/2 at low temperature ) and ZnFe₂O₄ ( S = 5/2 ), each of which has half-integer-spin transition metal ions. In both of these cases, the structural transitions are also closely associated with T_N, which suggests that distortions from cubic lattice symmetry generally occur at the Néel transitions in half-integer-spin magnetically frustrated spinels.

In light of these observations for half-integer-spin systems, it is interesting to speculate that the absence of a structural transition in GeNi₂O₄ may be a consequence of the integer-spin of the Ni^{2 +} ion. In one-dimensional antiferromagnets, spin-Peierls transitions for spin-1 magnetic ions are prevented by the appearance of Haldane gaps, which render the chains rigid against dimerization [ 7 ]. This raises the question of whether a related phenomenon can also exist in a three-dimensional integer-spin frustrated lattice, which naturally leads us to measurements of the spin excitations in the Néel state of GeNi₂O₄.

In Figure 3 we show the low temperature heat capacity of GeNi₂O₄. The data are superimposed with a fit including a contribution from gapless isotropic spin-waves and a gapped excitation located approximately = 11 K above the ground state. The gapped excitation in GeNi₂O₄ is a property of the Néel state in the cubic structure, and thus clearly requires a different explanation from the much higher energy excitation reported in tetragonal ZnCr₂O₄ [ 4, 6 ]. The absence of a structural phase transition in GeNi₂O₄ combined with the gapped magnetic excitation spectrum strongly suggests a direct connection between these phenomena and the integer spin of the Ni^{2 +} ion.

References:

[1] M. K. Crawford et al., Phys. Rev. Lett., submitted; M. K. Crawford et al., unpublished results.

[2] E. F. Bertaut et al., J. Phys. 25, 516 (1964).

[3] M. F. Collins and O. A. Petrenko, Can. J. Phys. 75, 605 (1997).

[4] S.-H. Lee, C. Broholm, T. H. Kim, W. Ratcliff, and S.-W. Cheong, Phys. Rev. Lett. 84, 3718 (2000).

[5] Y. Yamashita and K. Ueda, Phys. Rev. Lett. 85, 4960 (2000).

[6] O. Tchernyshyov, R. Moessner, and S. L. Sondhi, Phys. Rev. Lett. 88, 067203 (2002).

[7] F. D. M. Haldane, J. Appl. Phys. 57, 3359 (1985).

---

M. K. Crawford, R. L. Harlow, R. Flippen
DuPont Co., Wilmington, DE 19880-0356

P. L. Lee, Y. Zhang
Advanced Photon Source
Argonne National Laboratory, Argonne, IL 60439

J. Hormadaly
Ben Gurion University of the Negev
Beer Sheeva, Israel

Q. Huang, J. W. Lynn
NIST Center for Neutron Research
National Institute of Standards and Technology
Gaithersburg, MD 20899-8562

R. Stevens, B. F. Woodfield, J. Boerio-Goates
Brigham Young University, Provo, UT 84602

R. A. Fisher
Lawrence Berkeley National Laboratory
University of California, Berkeley, CA 94720

Back to FY2003 HTML main page
Go to previous article
Go to next article

To view all symbols correctly, please download Internet Explorer 6 or Netscape 7.1