Membrane phases are one example of the variety of complex fluid structures formed by surfactant molecules in solution. They are most commonly encountered in biological systems, but are also used extensively in a variety of commercial applications from personal care products to foods to paints. The diagram in Figure 1 shows the regularly stacked lamellae of the capital L sub alpha phase and the convoluted meandering channels of the “sponge” or capital L sub 3 phase. The topological distinctions between these two phases result in very different macroscopic properties. The anisotropic lamellar phases are birefringent and viscous, with complicated flow responses, while the isotropic sponge phases are clear and generally flow freely with constant viscosity. However, these very distinct phases are adjacent in the phase diagrams of many systems, and very dilute sponge phases exhibit a transient birefringence when shaken, which suggests a shear-induced transition to a lamellar state. Due to the experimental challenges of studying both the structure and rheology of such dilute phases, the exact nature of the transient birefringence has remained somewhat controversial.
Both sponge and lamellar structures have scaling properties: their characteristic lengths (see Figure 1), the channel width, xi, and the smectic periodicity, d, scale with the ratio of the membrane thickness, delta, to the membrane volume fraction, phi. The dynamics of these phases are dominated by thermodynamic fluctuations of the membranes, which also scale with these parameters. Cates and Milner predict the scaling relationship and shear response to be expected for an isotropic diblock copolymer phase (Refer to reference 1). They note that this phase is topologically similar to sponge phases, and therefore expect the relationship to extend to such systems as well. Their analysis indicates that flow should dampen fluctuations normal to both the flow velocity (vector V) and the velocity gradient (vector nabla V), eliminating channels in those directions. This would result in a quasi-first order phase transition to a lamellar state with its membranes parallel to the velocity velocity plane, i.e., perpendicular to Z, (conventionally the “a” orientation) occurring at a critical shear rate: gamma dot sub c is of order k sub B, times T, times the quantity, open parenthesis, phi over delta, close parenthesis, to power 3, all over eta sub s, where k sub B is the Boltzmann constant, T is the temperature, and eta sub s is the solvent viscosity.
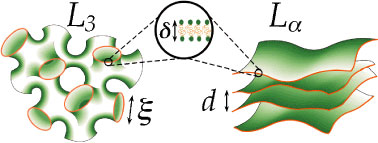
| Figure 1. Representations of two types of membrane morphologies: the sponge (L sub 3) and lamellar (L sub alpha) phases with their corresponding characteristic lengths. |
From the equation, it is clear that transient birefringence, occurring at low shear rates, requires very dilute samples, i.e., having small phi. Furthermore, the phi cubed over eta sub s dependence suggests that increasing solvent viscosity to slow membrane fluctuations would relax this requirement. Taking our lead from previous microemulsion work (Refer to reference 2), we found that dextrose could be dissolved at volume fractions up to 40 % in the heavy brine solvent (0.2 mol of sodium chloride in deuterated water to make a 1 liter solution) of cetylpyridinium chloride/hexanol membrane systems without altering their phase diagrams. The maximum dextrose addition changes eta sub s from 1.1 milli pascal seconds to 13.6 milli pascal seconds. Then for a series of sponge samples having membrane volume fractions from 3 % to 10 %, the factor phi cubed over eta sub s can be varied by more than two orders of magnitude. Plots of the reduced viscosity and shear stress (Figure 2 B) versus the rescaled shear rate parameter, gamma dot, times eta sub s, over phi cubed, display master curve behavior, clearly showing that these macroscopic responses measuring the dynamics of this system scale as predicted. The corresponding scaled micro-structural response parameters, explored by Couette, S A N S, (Figure 2 C and D), likewise exhibit excellent scaling behavior. Moreover, the strong correlation between these macroscopic and microscopic responses leads to a detailed picture of the mechanisms involved.
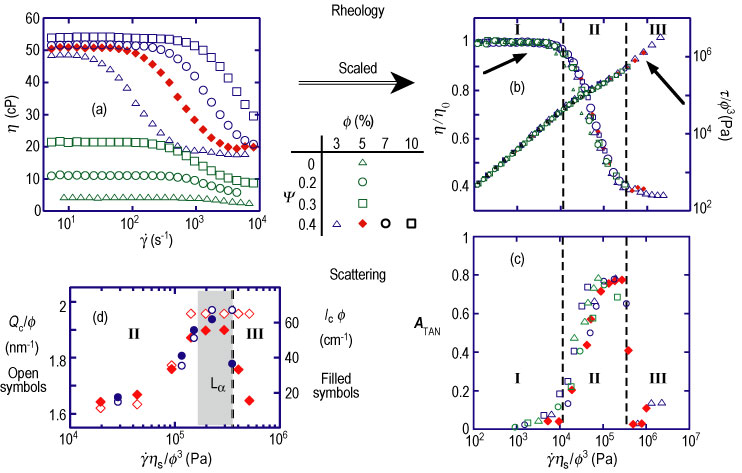
| Figure 2. (A) Rheological data for a range of membrane volume fractions (phi) and dextrose concentrations (psi). (B) The same plotted to show master curve behavior, indicative of scaling. (C) The corresponding master curve variation of the scattering anisotropy, A, sub TAN, is identically equal to open parenthesis, I sub z, minus I sub gradient v, close parenthesis, over, open parenthesis, I sub z, plus I sub gradient v, close parenthesis, and (D) the rescaled correlation peak position and intensity. Regions I, II and III are discussed in the text. |
The response exhibits three distinct regions (Refer to reference 3). (See Figures 2 and 3) At low shear rates (Region I), the sponges show their familiar constant viscosity Newtonian behavior and isotropic scattering. No structural changes occur since the applied shear rate is much less than the dynamic response rate of the channels. In region II, when the shear rate approaches this rate, the density of connections in the gradient direction (vector nabla V) decreases, leading to a gradual development of smectic order in that direction, and thus causing the observed decrease in viscosity. At shear rates high enough to totally eliminate the channels along vector nabla V the intensity I sub vector nabla V saturates, indicating the appearance of a lamellar phase with the membranes fully-aligned parallel to Z. In view of the theory, this is an unexpected result: the order develops in the so-called “c” orientation, indicating that it is fluctuations in the gradient direction (vector nabla V) that are being suppressed rather than in the vorticity (Z) direction of the predicted “a” orientation. Also the complete lack of a rheological stress plateau (Figure 2 A) and the gradual change of the peak position (Figure 2 D) both preclude the possibility of the transition being first order. The aligned lamellar phase remains stable over only a narrow range of shear rates in region II before collapsing at the onset of region III to a structure with correlations on length scales much grater than xi, which is only observed for samples with sufficiently high solvent viscosities and low membrane concentrations. While more work remains to determine the nature of this final structure, we note that it has been predicted that suppression of fluctuations by shear should eventually destabilize a bulk lamellar system (Refer to reference 4).
While the magnitude of the critical shear rates are consistent with theory and we have now confirmed the scaling behavior of the shear response, the nature of the transition and the orientation of the shear-induced smectic state are not as predicted. The theory does not, in fact, extend straightforwardly to the topologically similar sponge phases as expected, and a more sophisticated model is needed to fully explain the details of shear response in this class of systems.
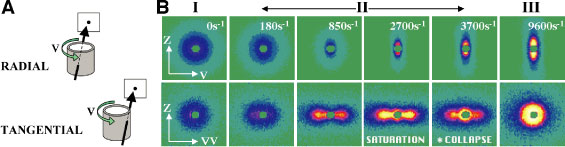
| Figure 3. (A) Schematic of the beam incidence on the Couette S A N S cell in radial and tangential geometries. (B) Scattering patterns in radial and tangential geometries for a phi = 0.05, psi = 0.4 sponge sample at a range of shear rates over the three rheological regions. |
References
[1] M. E. Cates and S. T. Milner, Phys. Rev. Lett. 62, 1856 (1989).
[2] Chen V., PhD Thesis, University of Minnesota (1988).
[3] L. Porcar et al., Phys. Rev. Lett., in press.
[4] S. Ramaswamy, Phys. Rev. Lett. 69, 112 (1992), and R. Bruinsma and Y. Rabin, Phys. Rev. A 45, 994 (1992).
Authors
L. Porcar
Oak Ridge National Laboratory
Oak Ridge, TN 37831-6393
Present address:
University of Maryland
College Park, MD 20742
W. A. Hamilton and P. D. Butler
Oak Ridge National Laboratory
Oak Ridge, TN 37831-6393
G. G. Warr
The University of Sydney
Sydney, NSW 2006, Australia
Back to FY2002 HTML main page
Go to next article
To view all symbols correctly, please download Internet Explorer 6 or Netscape 7.1