
|

|
|
| Home | Live Data | Instruments | CHRNS | Proposals |
Scattering Length Density Calculator
This calculator will stop working in newer installs of Java. Please update your bookmark to the newer version of SLD calculator developed by Paul Kienzle at http://www.ncnr.nist.gov/resources/activation/. This one calculates estimates of neutron activation and uses newer cross sections as well.
Usage notes:
NOTE: The above neutron cross section calculations are only for thermal neutron cross sections. I do not have any energy dependent cross sections. For energy dependent cross sections please go to the National Nuclear Data Center at Brookhaven National Lab.
The neutron scattering length density is defined as:

The corresponding quantity for x rays is obtained by replacing the bc values in the expression by Zre, where re = 2.81 x 10-13 cm, is the classical radius of the electron, and Z is the atomic number of the ith atom in the molecular volume vm.
To calculate scattering length densities enter a compound and a mass density and click "Calculate". The first calculation will take the longest because the program has to download all of the data tables of neutron and x-ray scattering lengths, but it should be faster after that is performed.
It is not necessary to enter a number into the wavelength field. The wavelength is used to calculate the absorption cross section. The default wavelength is 1.8 Angstroms. If a value is entered into this field the absorption cross section will be scaled as wavelength/1.8 since the cross section data is given for 1.8 Angstrom (2200 m/s, 0.0253 eV, thermal) neutrons.
Specific isotopes are specified by putting the mass number in parenthesis after the symbol.
Element Symbols are case sensitive.
Only integer stoichiometry is supported at this time. If there is sufficient interest I will add non-integer stoichiometry. Until it is added you can use factors of 10 to do non-integer stoichiometry. For instance if you wanted to calculate Pd1.3Si you can enter it as Pd13Si10, and as long as the density is correct it will calculate it correctly.
Examples of how to format the compound name:
- SiO2 (silicon dioxide)
- H20 (water)
- H(2)2O (heavy water), can also be written as D2O
- A 50% mixture of H2O and D2O can be calculated as follows: The mass densities of H2O and D2O are 1.0 and 1.1 g/cm^3, respectively. A 50-50 mixture of the two would then have a mass density of 1.05 g/cm^3. Write this mixture of H2O and D2O as H2OD2O or more simply as HDO. Other compositions can be calculated as well, for example a 70-30 mixture of H2O/D2O can be written as H14O7D6O3 or more simply H7D3O5 (i.e. 7 hydrogens, 3 deuteriums, and 5 oxygens) and the mass density calculated based on the percentages of H and D.
- C(13)6H(2)12O(18)6 (6 Carbon-13 atoms, 12 deuterium atoms, and 6 Oxygen-18 atoms)
To see what isotopes can be included in these calculations look at Neutron Scattering Lengths and Cross Sections on the web. All of the isotopes contained in that site are included in this calculator.
The 1/e length is the thickness of material that will attenuate a neutron beam to 1/e (about 0.37) of its incident intensity. It is calculated as
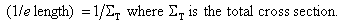
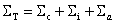
and Sigmac and Sigmai are the coherent and incoherent scattering cross sections, respectively, per unit volume (in units of cm-1), and Sigmaa is the absorption cross section per unit volume. These cross sections are computed from the corresponding tabulated atom cross sections, i.e.,
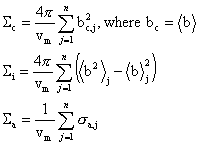
Caveats: The coherent and incoherent cross sections are calculated from the bound scattering lengths for nuclei. The actual cross sections depend on the incoming neutron energy and sample temperature, especially for light elements. For low energy neutrons (cold neutrons), the tabulated cross sections are generally a lower limit. The measured incoherent scattering from hydrogen, for example, can be considerably larger (by more than 20%) than its bound value.
For example, the incoherent scattering cross section of H2O is
![Sigma_i(H2O) = 5.36cm^-1 calculated from tables[1] of scattering lengths, Sigma_i(H2O) = 7.0cm^-1 from measured cross section for 5 meV neutrons at 290K](./sldimage010.gif)
The macroscopic incoherent cross section calculated above includes no information about the structure of the material. It does not include what some call the "compositional" or "mixture" incoherent scattering which is due to nuclei (either different elements or isotopes) with different coherent scattering lengths being randomly distributed throughout a material. A better term for this type of scattering is "diffuse coherent scattering."
If you want to calculate that "diffuse coherent scattering" term because you'd like to see how much it would add if your material was perfectly disordered you can get it by following the very clear instructions in reference [3] below in which it is called the "Laue monotonic scattering."
For further discussion of this point see refs. [2,3].
[1]"Neutron scattering lengths and cross sections," V.F. Sears, Neutron News 3, No. 3, 26-37 (1992).
[2]"The forward scattering of cold neutrons by mixtures of light and heavy water," R.P. May, K. Ibel and J. Haas J. Appl. Cryst. 15, 15-19 (1982). [3]"Incoherent Scattering from Multi-Element Materials," C.J. Glinka, J. Appl. Cryst 44, 618-624 (2011).
Report errors or make inquiries to Alan Munter, <[email protected]>
Last modified 28-January-2014 by website owner: NCNR (attn: Alan Munter)